Triskaidekaphilia (Part II)

6. 13 is a prime such that for any digits a,b > 0 and any integers n,m > 1 one can build an integer divisible by it having exactly n digits equal to a, exactly m digits equal to b and exactly 2 digits equal to 0. Moreover this m+n+2 digit long number is non-trivial, in that none of the two 0 digits is located at the end of the number.

Indeed this is true since:
\(13 \mid 10\underbrace{1 \ldots 1}_{k \; times \; 1}01, \forall k \in \mathbf{N}\)

One other prime with this property is 7. This can easily e extended to any number of digits.

7. 13 is a prime with the property that:

\( \forall a,b \in \mathbf{N} \; \left\{ \begin{array}{l} p \mid \overline{ab} \\ p \mid \overline{bc} \end{array} \right. \rightarrow p \mid \overline{ca} \)

This is equivalent to the fact that the following equation system in a, b and c:

\( \left\{ \begin{array}{ccccccc} 10 \cdot a & + & 1 \cdot b & + & 0 \cdot c & = & 0 \\ 0 \cdot a & + & 10 \cdot b & + & 1 \cdot c & = & 0 \\ 1 \cdot a & + & 0 \cdot b & + & 10 \cdot c & = & 0 \end{array} \right. \)

has non-trivial solutions modulo p, hence for its discriminant we have that:

\( \left| \begin{array}{ccc} 10 & 1 & 0 \\ 0 & 10 & 1 \\ 1 & 0 & 10 \end{array}\right| = 1001 \equiv 0 \mod{p} \)

Therefore the primes with this property are 7, 11 and 13.

8. 13 is a prime with the property that:

\(\forall a,b \in \mathbf{N} \; \left\{ \begin{array}{l} p \mid \overline{ab} \\ p \mid \overline{bc} \end{array} \right. \rightarrow p \mid a + b + c\)

9. 13 is a prime with the property that:

\(\forall a,b \in \mathbf{N} \; \left\{ \begin{array}{l} p \mid \overline{ab} \\ p \mid \overline{bc} \end{array} \right. \rightarrow p \mid a^2 + b^2 + c^2\)

Triskaidekaphilia (Part I)

As Discrete Connections will turn soon 13 (for those frail at heart, please do stay away, you may never know what may happen :P), I decided to start another thread concerning, as you might have guessed, the arithmetic properties of number 13 (and other prime numbers to that respect), some old, some fresh, but altogether hopefully increasingly interesting. Wherever possible open questions will be raised, and extensions for other prime numbers will be mentioned (please forgive me if I fail in finding references to some of the results to follow, it is not intentional but merely a proof I'm not nor ever will be a know-it-all).

1. 13 is a prime number.

This should have not come as a surprise, but I ought have mentioned it as it one of the basic properties of this number.

2. 13 is a prime that can be written as a sum of squares of natural numbers.

Indeed:

[; 13 = 2^2 + 3^2;]

It is not the first prime having this property:

[;2 = 1^2 + 1^2, \; 5 = 1^2 + 2^2;]

but it's the first for which the squared numbers are also primes. Are there an infinity of such primes? Yes as this is a consequence the renowned sum of squares theorem attributed to Fermat stating that this property holds for a prime if and only if that prime is congruent to 1 modulo 4. Since there are an infinity of those, thanks to Dirichlet's theorem stating that any arithmetic progression having relatively prime first term and ratio contain an infinity of primes (1 and 4 are such numbers), the conclusion follows naturally.

3. 13 is a prime that divides the sum of squares of all the previous prime numbers.

Indeed:

[;2^2 + 3^2 + 5^2 + 7^2 + 11^2 = 208 = 13 \cdot 16;]

Here 13 is definitely the first prime with this property. Is it the only one, are there infinitely more such primes? Hard to answer (in my opinion very unlikely).

4. 13 is a prime belonging to the Fibonacci sequence.

Not the first (2,3 and 5 are also), not the last, just one of the many (not yet known if there are infinitely many, but there are some big ones).

5. 13 is a prime with the property that:

[;\tau_2(p) = p-2;]

where the notation follows Discrete connections (the euclidean summation peak).

Here there are as many primes as in 4 since:

[;\tau_2(n) = n-2 \Leftrightarrow \exists m \in \mathbf{N} \; such \; that \; n = F_{m} \ge 2;]

Discrete connections (part XII)

First a small stop to explain this sudden "gold rush" about finite continued fractions and how they impact upon the subject at stake.

1. As mentioned previously, they are related to the euclidean fractal by its construction. Indeed, consider:

[; the \; (p_{s}-1)^{th} \; block \; of \; \ldots \; of \; the \; (p_{1}-1)^{th} \; block \; of ;]
[; the \; euclidean \; fractal \; defined \; by \; u=0, v=i, w=1+i, z=1 ;]

then its base endpoints' real parts are:

[;\cfrac{1}{p_1+\cfrac{1}{\ddots + \cfrac{1}{p_s}}}} \; and \; \cfrac{1}{p_1+\cfrac{1}{\ddots + \cfrac{1}{p_s + 1}}}};]

2. As you might already know, any positive rational number can be expressed as a continued fraction whose components are, in a top-down representation, the successive quotients obtained through Euclid's gcd algorithm applied to the numerator and denominator. Moreover, there is only one such canonical representation, i.e. if a sub-unitary rational number k/n is equal to a canonical finite continued fraction then we have all the steps of Euclid's gcd algorithm (we have all the quotients) for n and k.

Further more, if we strictly bound a positive sub-unitary rational number k/n to values such as described in 1, then Euclid's gcd algorithm for n and k has at least s steps, for which the quotients are given by the continued fractions defining the boundaries.

Discrete connections (part XI)

This part can be better classified as a "bigger picture" overview. We've seen in the past articles several strong hints concerning the global properties of the euclidean summation but no word yet about local ones. Here we try to give some of these local properties a go, while raising subtle bridges between the euclidean summation and the euclidean fractal.

As accustomed, we will define some derivatives of the euclidean summation peak and euclidean summation positional peak:

[; \tau_2^{p}(n) = \left\{ \begin{array}{l} 0, \; if \; I_n^{p} = \emptyset \\ \max\{ \tau_1(n,k) \; | \; k \in I_{n}^{p} \}, \; otherwise \end{array} \right. ;]

[; \tau_3^{p}(n) = \left\{ \begin{array}{l} 0, \; if \; I_{n}^{p} = \emptyset \\ \max\{ k \in I_{n}^{p} \; | \; \tau_1(n,k) = \tau_2^{p}(n) \}, \; otherwise \end{array} \right. ;]

where:

[; p \in \mathbf{N}, \; p \ge 1 ;]

[; I_{n}^{p} = \{k \in \mathbf{N} \; | \; \frac{n}{p+1} \le k \le \frac{n}{p} \} ;]

The target conjectures for these derivatives are:

[; \lim_{n \rightarrow \infty} \frac{\tau_2^{p}(n)}{n} = \frac{\varphi}{p + \phi} ;]

[; \lim_{n \rightarrow \infty} \frac{\tau_3^{p}(n)}{n} = \frac{1}{p+\phi} ;]

For p=1 these conjectures translate to the result proven for the euclidean summation peak and respectively to the conjecture for the euclidean summation positional peak.

We can go even deeper with this construction, and involve yet another classic: continued fractions (and thus tighten the links with the euclidean fractal). Indeed:

[; \forall s \in \mathbf{N}, \; s > 0 \; and \; \forall w = (p_1, \ldots, p_s) \in (\mathbf{N} \setminus \{0\})^{s} ;]

let us define:

[; \tau_2^{w}(n) = \left\{ \begin{array}{l} 0, \; if \; I_n^{w} = \emptyset \\ \max\{ \tau_1(n,k) \; | \; k \in I_{n}^{w} \}, \; otherwise \end{array} \right. ;]
[; \tau_3^{w}(n) = \left\{ \begin{array}{l} 0, \; if \; I_{n}^{w} = \emptyset \\ \max\{ k \in I_{n}^{w} \; | \; \tau_1(n,k) = \tau_2^{w}(n) \}, \; otherwise \end{array} \right. ;]

where

[; I_{n}^{w} = \{k \in \mathbf{N} \; | \; \cfrac{n}{p_1+\cfrac{1}{\ddots + \cfrac{1}{p_s + \epsilon(s)}}}} \le k \le \cfrac{n}{p_1+\cfrac{1}{\ddots + \cfrac{1}{p_s + 1 - \epsilon(s)}}}} \} ;]

and:

[;\epsilon(s) = \left\{ \begin{array}{l} 0, \; if \; s \; even \\ 1, \; otherwise \end{array} \right. ;]

The conjectured results for these generalized derivatives are:

[; \lim_{n \rightarrow \infty} \frac{\tau_3^{w}(n)}{n} = \cfrac{1}{p_1+\cfrac{1}{\ddots + \cfrac{1}{p_s + \phi }}} ;]

Next: To be continued ...

Discrete connections (part X)

From this part on we strive to define candidates for the left and right mappings from both the euclidean summation and the euclidean fractal point of view.
Let us define by the left and right mappings of the normalized euclidean summation the functions conjectured to have the following properties:

D)

[;\varepsilon^{\tau}_{l}, \varepsilon^{\tau}_{r}:(0,1) \rightarrow [0,1];]
L)
[;\varepsilon^{\tau}_{l}(x)=\lim_{n \rightarrow \infty}\frac{\tau_1(n,\lceil x \cdot n \rfloor)}{n};]
R)
[;\varepsilon^{\tau}_{r}(x)=\lim_{n \rightarrow \infty}\frac{\tau_1(n,\lfloor x \cdot n \rceil)}{n};]

where:

[;\lceil x \rfloor = \lceil x \rceil - 1;]

[;\lfloor x \rceil = \lfloor x \rfloor + 1;]

Given the properties of the euclidean summation, for the moment we can prove only:

- that D) is well defined, since:

[;0 < \tau_1(n,k) < n;]

and both the lower and the upper bounds are reached;

- that the sequences in L) and R), due to their boundedness, both contain convergent subsequences.

We can of course prove the above for discrete cases:

[; x = \frac{1}{p}, \; where \; p \in \mathbf{N}, p \ge 2 ;]

For proving L, if p divides n we have:

[; n = k \cdot p \Rightarrow \lceil n \cdot x \rfloor = k - 1 \Rightarrow n = p \cdot (k-1) + p ;]

which becomes a valid euclidean division (with quotient p and remainder p), if  k-1>p. Since we are dealing with a limit, this assumption is safe.

Now on the other hand we get:

[; \tau_1(n,k-1) = p + \tau_1(k-1, p) \Rightarrow ;]

[; 0 < \tau_1(n, k-1) < p + \max\{r + \tau_1(p,r) | r \in \mathbf{N}, r < p \} \Rightarrow;]

[; 0< \tau_1(n, k-1) < 3 \cdot p \Rightarrow \lim_{n \rightarrow \infty, \; p|n}} \frac{\tau_1(n, \lceil n \cdot \frac{1}{p} \rfloor)}{n} = 0 ;]

If p does not divide n then we have:

[; n = k \cdot p + r, \; where \; r \in \mathbf{N}, \; 0<r<p \Rightarrow ;]

[; \lceil n \cdot x \rfloor = k \Rightarrow n = p \cdot k + r ;]

which becomes a valid euclidean divison if k>p.

In a similar fashion as above we get:

[; 0 < \tau_1(n,k) < 3 \cdot r \Rightarrow 0 < \tau_1(n,k) < 3 \cdot p \Rightarrow ;]

[; \lim_{n \rightarrow \infty, p \nmid n} \frac{\tau_1(n, \lceil n \cdot \frac{1}{p} \rfloor)}{n} = 0 ;]

For proving R we can use the general case:

[; n = k \cdot p + r, \; where \; r \in \mathbf{N}, \; 0 \le r < p \Rightarrow ;]

[; \lfloor n \cdot x \rceil = k+1 \Rightarrow n = (p-1) \cdot (k+1) + k + 1 - p + r ;]

which becomes a valid euclidean division if k>p.

Therefore:

[; \tau_1(n, k + 1) = k + 1 - p + r + \tau_1(k + 1, k + 1 - p + r) ;]

If we raise the boundary of k we get:

[; k > 2 \cdot p \Rightarrow ;]

[; \tau_1(n, k + 1) = k + 1 + \tau_1(k + 1 - p + r, p - r) \Rightarrow ;]

[; k + 1 \le \tau_1(n, k + 1) < k + 1 + 2 \cdot (p - r) \Rightarrow ;]

[; k + 1 \le \tau_1(n, k + 1) < k + 1 + 2 \cdot p \Rightarrow ;]

[; \lim_{n \rightarrow \infty} \frac{\tau_1(n, \lfloor n \cdot \frac{1}{p} \rceil )}{n} = \frac{1}{p} ;]

Thus we have proven not only that L and R are well defined for x=1/p but that the limits obtained make some of the conjectured properties of the left and right mappings true.

Next: One step deeper ...

Discrete connections (part IX)

First let us extend B) to (0,1).
[;Case\;  x = \frac{1}{2};]
I this case we have:

[;\left\{\begin{array}{rcl}\varepsilon_l(\frac{1}{2}) & = & 0 \\ (1 + p \cdot \frac{1}{2}) \cdot \varepsilon_l(\frac{\frac{1}{2}}{1+p\cdot \frac{1}{2}}) & = & 0 \\ \varepsilon_r(\frac{1}{2}) & = & \frac{1}{2} \\ (1 + p \cdot \frac{1}{2}) \cdot \varepsilon_r(\frac{\frac{1}{2}}{1 + p \cdot \frac{1}{2}}) & = & \frac{1}{2}\end{array}\right.;]

hence the conclusion.

[;Case \; x \in (0, \frac{1}{2});]

For p=0 we are left to prove an identity.

In the other subcases we have:

[;x \in (0,\frac{1}{2}) \Rightarrow (1-x) \in (\frac{1}{2},1) \Rightarrow^{C)};] 

[; \left\{\begin{array}{rcl} \varepsilon_l(1-x) & = & (1 + p \cdot x) \cdot \varepsilon_l(\frac{1+(p-1)\cdot x}{1 + p \cdot x}) \\ \varepsilon_r(1-x) & = & (1+p \cdot x) \cdot \varepsilon_r(\frac{1 + (p-1) \cdot x}{1 + p \cdot x}) \end{array} \right. ;]

For p greater or equal to 1 we get:

[;\frac{x}{1 + p \cdot x} \in (0,\frac{1}{2}) \Rightarrow;]

[;\frac{1+ (p-1) \cdot x}{1 + p \cdot x} \in (\frac{1}{2},1);]

Therefore:

[;\left\{ \begin{array}{rcl}\varepsilon_l(1-x) & = & x + \varepsilon_r(x) \\ \varepsilon_r(1-x) & = & x + \varepsilon_l(x) \\ \varepsilon_l(\frac{1+(p-1) \cdot x}{1 + p \cdot x}) & = & \frac{x}{1+p\cdot x} + \varepsilon_r(\frac{x}{1 + p \cdot x}) \\ \varepsilon_r(\frac{1+(p-1) \cdot x}{1 + p \cdot x}) & = & \frac{x}{1+p \cdot x} + \varepsilon_l(\frac{x}{1+p \cdot x})\end{array}\right.;]

hence the conclusion.

Having this proved we can state a substitute result for A):

A') (outer row recurrence)
[;\forall x \in (\frac{1}{2},1), \left\{\begin{array}{rcl} \varepsilon_l(x) & = & (1-x) + x \cdot \varepsilon_r(\frac{1-x}{x}) \\ \varepsilon_r(x) & = & (1-x) + x \cdot \varepsilon_l(\frac{1-x}{x}) \end{array}\right.;]

This holds since B) for (1-x) and p=1 implies:

[;\left\{\begin{array}{rcl}\varepsilon_l(1-x) & = & x \cdot \varepsilon_l(\frac{1-x}{x}) \\ \varepsilon_r(1-x) & = & x \cdot \varepsilon_r(\frac{1-x}{x}) \end{array}\right.;]

Now we can focus on the corner stone result for the left and right mappings:

[;\varepsilon_l(x) = 1 \; or \; \varepsilon_r(x) = 1 \Rightarrow x=\phi;]

Let x be a value such that the upper bound of either the left or the right mapping is reached. This value is different than 1/2 since:

[;\left\{ \begin{array}{rcl}\varepsilon_l(\frac{1}{2}) = 0 \\ \varepsilon_r(\frac{1}{2}) = \frac{1}{2}\end{array}\right.;]

Moreover x is greater than 1/2 since otherwise we would get:

[;\varepsilon_r(1-x) & = & 1 + x > 1;]

or

[;\varepsilon_l(1-x) & = & 1 + x > 1;]

thus contradicting 0).

From A') results that:

[;\varepsilon_r(\frac{1-x}{x}) = 1;]

or

[;\varepsilon_l(\frac{1-x}{x}) = 1;]

By mathematical induction one can prove that:

[;\varepsilon_l(\frac{(-1)^{k+2}\cdot F_{k+1} + (-1)^{k+3} \cdot F_{k+2} \cdot x}{(-1)^{k+1}\cdot F_{k} + (-1)^{k+2} \cdot F_{k+1} \cdot x})=1;]
or
[;\varepsilon_r(\frac{(-1)^{k+2}\cdot F_{k+1} + (-1)^{k+3} \cdot F_{k+2} \cdot x}{(-1)^{k+1}\cdot F_{k} + (-1)^{k+2} \cdot F_{k+1} \cdot x})=1;]

Since all values of x for which the upper bound of either the left or the right mapping is reached fall between 1/2 and 1 results that x is bounded successively by ratios of consecutive elements of the Fibonacci sequence, hence the conclusion.

The principle behind the proof (bounding values to Fibonacci ratios) was already applied in part IV and part VII, thus confirming again the strong connection between the mathematical concepts described throughout the paper.

Next: Left and right mapping candidates.

Discrete connections (part VIII)

This part deals with a class of conjectured mappings strongly connected to the euclidean summation and its properties.
Indeed, let us define by the euclidean left and right mappings the functions having the following properties:

0) (definition and upper boundary)

[;\varepsilon_l,\varepsilon_r:(0,1)\rightarrow [0,1];]

A) (inner row recurrence)

[;\forall x \in (\frac{1}{2},1), \left\{\begin{array}{rcl}\varepsilon_l(x) & = & (1-x) + \varepsilon_r(1-x) \\ \varepsilon_r(x) & = & (1-x) + \varepsilon_l(1-x) \end{array} \right.;]
B) (column periodicity)
[;\forall x\in (\frac{1}{2}, 1), \forall p \in \mathbf{N}, \left\{\begin{array}{rcl}\varepsilon_l(x) & = & (1+p\cdot x) \cdot \varepsilon_l(\frac{x}{1+p\cdot x})\\ \varepsilon_r(x) & = & (1 + p \cdot x) \cdot \varepsilon_r(\frac{x}{1+p \cdot x})\end{array}\right.;]
C) (diagonal periodicity)
[;\forall x\in (\frac{1}{2}, 1), \forall p \in \mathbf{N}, \left\{\begin{array}{rcl}\varepsilon_l(x) & = & ((p+1)-p\cdot x) \cdot \varepsilon_l(\frac{p - (p-1) \cdot x}{(p+1)-p\cdot x})\\ \varepsilon_r(x) & = & ((p+1) - p \cdot x) \cdot \varepsilon_r(\frac{p - (p-1) \cdot x}{(p+1)-p \cdot x})\end{array}\right.;]
D) (lower boundary)
[;\forall p \in \mathbf{N}, \; p \ge 2, \left\{ \begin{array}{rcl} \varepsilon_l(\frac{1}{p}) & = & 0 \\ \varepsilon_r(\frac{1}{p}) & = & \frac{1}{p} \end{array}\right.;]

First some basic properties of these functions:

E) (upper boundary is achieved)

[;\varepsilon_l(\phi)=\varepsilon_r(\phi)=1;]

D')
[; \forall p \in \mathbf{N}, \; p \ge 2 \left\{\begin{array}{rcl}\varepsilon_l(\frac{p-1}{p})=\frac{2}{p}\\ \varepsilon_r(\frac{p-1}{p})=\frac{1}{p}\end{array}\right.;]

For the second property the proof requires only to apply A) and D). For the first the proof takes the following steps:

[;B) \; for \; x=\phi, \; p=1 \Rightarrow \left\{\begin{array}{rcl}\varepsilon_l(\phi) & = & (1+\phi) \cdot \varepsilon_l(\frac{\phi}{1+\phi})\\ \varepsilon_r(\phi) & = & (1+\phi) \cdot \varepsilon_r(\frac{\phi}{1+\phi}) \end{array}\right. \Rightarrow ;]

[;\left\{\begin{array}{rcl}\varepsilon_l(\phi) & = & \varphi \cdot \varepsilon_l(1-\phi) \\ \varepsilon_r(\phi) & = & \varphi \cdot \varepsilon_r(1-\phi) \end{array}\right. \Rightarrow^{A)} \left\{ \begin{array}{rcl}\varepsilon_l(\phi) & = & \varphi \cdot (\varepsilon_r(\phi) - \phi^2) \\ \varepsilon_r(\phi) & = & \varphi \cdot (\varepsilon_l(\phi) - \phi^2)\end{array}\right. \Rightarrow;]

[;\left\{\begin{array}{rcl}(1+\varphi) \cdot \varepsilon_l(\phi) & = & (1+\varphi) \cdot \varepsilon_r(\phi) \\ \varepsilon_r(\phi) & = & \varphi \cdot (\varepsilon_l(\phi) - \phi^2) \end{array}\right. \Rightarrow ;]

[;\left\{\begin{array}{rcl}\varepsilon_l(\phi) & = & \varepsilon_r(\phi) \\ \varphi \cdot \varepsilon_l(\phi) - \varepsilon_r(\phi) & = & \phi \end{array}\right. \Rightarrow \left\{\begin{array}{rcl} \varepsilon_l(\phi) & = & \varepsilon_r(\phi) \\ \varepsilon_r(\phi) & = & 1 \end{array} \right.;]

Although expanding A) to values smaller than 1/2 is not trivial, this can be achieved for B), but after some intermediate result:

F) (unifying formula)

[;\forall x \in (0,1), \left\{ \begin{array}{rcl} \varepsilon_l(x) + x & = & (1+x) \cdot \varepsilon_r(\frac{1}{1+x}) \\ \varepsilon_r(x) + x & = & (1+x) \cdot \varepsilon_l(\frac{1}{1+x}) \end{array} \right.;]

The proof follows the relative positions of x and 1/2.

[;Case \; x \in (\frac{1}{2},1);]

In this case we get successively:

[;x \in (\frac{1}{2},1) \Rightarrow x \in (0,1) \Rightarrow \frac{1}{1+x} \in (\frac{1}{2},1) \Rightarrow^{A)};]

[;\left\{ \begin{array}{rcl} \varepsilon_l(\frac{1}{1+x}) & = & \frac{x}{1+x} + \varepsilon_r(\frac{x}{1+x}) \\ \varepsilon_r(\frac{1}{1+x}) & = & \frac{x}{1+x} + \varepsilon_l(\frac{x}{1+x}) \end{array} \right.;]

On the other hand from B) for x and p=1 we get:

[;\left\{\begin{array}{rcl} \varepsilon_l(x) & = & (1+x) \cdot \varepsilon_l(\frac{x}{1+x}) \\ \varepsilon_r(x) & = & (1+x) \cdot \varepsilon_r(\frac{x}{1+x}) \end{array}\right.;]

hence the conclusion.
[;Case \; x=\frac{1}{2};]
Indeed one has:

[;\left\{\begin{array}{rcl}(1 + \frac{1}{2}) \cdot \varepsilon_r(\frac{1}{1+\frac{1}{2}}) & = & \frac{1}{2} \\ \varepsilon_l(\frac{1}{2}) + \frac{1}{2} & = & \frac{1}{2}\\ (1 + \frac{1}{2}) \cdot \varepsilon_l(\frac{1}{1+\frac{1}{2}}) & = & 1 \\ \varepsilon_r(\frac{1}{2}) + \frac{1}{2} & = & 1 \end{array}\right.;]

hence the conclusion.

[;Case \; x \in (0, \frac{1}{2});]

In this case we get successively:

[;x \in (0, \frac{1}{2}) \Rightarrow (1-x) \in (\frac{1}{2},1) \Rightarrow^{A)} \left\{ \begin{array}{rcl} \varepsilon_l(1-x) & = & x + \varepsilon_r(x) \\ \varepsilon_r(1-x) & = & x + \varepsilon_l(x) \end{array}\right.;]

On the other hand from C) for 1-x and p=1 we get:

[;\left\{\begin{array}{rcl}\varepsilon_l(1-x) & = & (1+x) \cdot \varepsilon_l(\frac{1}{1+x}) \\ \varepsilon_r(1-x) & = & (1+x) \cdot \varepsilon_r(\frac{1}{1+x}) \end{array}\right.;]

hence the conclusion.
Next: Extra properties of the left and right mappings.

Discrete connections (part VII)

Starting with this part, we will deal with adjacent theories developed in order to shed some light on several of the asymptotic properties of the euclidean summation. Let us consider the following result:

[;\forall (x_n)_{n\ge 1} \subseteq \mathbf{N} \; the \; following \; assertions \; are \; equivalent;]

a)

[;\exists n_0 \in \mathbf{N} \; such \; that \; \frac{n}{2}<x_n<n, \; \forall n\ge n_0 \; and \lim_{n\rightarrow \infty}\frac{x_n + x_{x_n}}{n}=1;]

b)

[;\lim_{n\rightarrow \infty} \frac{x_n}{n} = \phi;]

Let us first prove that a) implies b). Indeed, since:

[;\frac{1}{2}<\frac{x_n}{n}<1, \; \forall n\ge n_0;]

results that the sequence is bounded, hence we can extract a convergent subsequence such as:

[;(k_n)_{n\ge 1} \; strictly \; increasing \; and \; (\frac{x_{k_n}}{k_n})_{n\ge 1} \rightarrow x;]

Through some computation (long but fairly simple) results that:

[;(\frac{x_{x_{k_n}}}{x_{k_n}})_{n \ge 1} \rightarrow \frac{1-x}{x};]

But out of this sequence we can extract a canonical subsequence such as:

[;(l_n)_{n\ge 1} \; strictly \; increasing \; and \; (\frac{x_{l_n}}{l_n})_{n\ge 1} \rightarrow \frac{1-x}{x};]

Therefore we will get successively the limits:

[;x, \frac{1-x}{x}, \ldots, \frac{(-1)^{k+2}\cdot F_{k+1} + (-1)^{k+3} \cdot F_{k+2} \cdot x}{(-1)^{k+1}\cdot F_{k} + (-1)^{k+2} \cdot F_{k+1} \cdot x}, \ldots;]

Since all of them must fall between 1/2 and 1 we get that x is bounded successively by consecutive ratios  of Fibonacci numbers, hence x equals the golden ratio conjugate.

The other implication (b) implies a)) is straightforward.

From now on we will call a Fibonacci decomposition of n any sequence verifying either a) or b).
The set of such sequences is non void since:

[;x_n=\lfloor n \cdot \phi \rfloor;]

and

[;y_n=\lceil n \cdot \phi \rceil;]

both verify b).

On the other hand, this class of sequences provides a tool for proving the conjectured asymptotic nature of the positional peek, i.e. we are left to prove that:

[;\lim_{n \rightarrow \infty} \frac{\tau_3(n) + \tau_3(\tau_3(n))}{n} = 1;]

Next: Left and right euclidean mappings

Discrete connections (part VI)

The main block of the euclidean fractal
For any four complex numbers u,v,w and z shaping a trapezoid let us consider the entity defined by the following elements:

the two base endpoints

[; u \; and \; z;]

the two top endpoints

[;v \; and \; w;]

the top line

[;\delta(v,w);]

the parallelism master line

[;\delta(u,v);]

the top value

[;\beta \in \sigma(v,w) \; such \; that \; \delta(\alpha,\beta) \| \delta(u,v);]

where:

[;\delta(z_1,z_2) \; - \; the \; complex \; line \; defined \; by \; z_1 \; and \; z_2;]

[;\sigma(z_1,z_2) \; - \; the \; open \; complex \; line \; segment \; defined \; by \; z_1 \; and \; z_2;]

[;\alpha \; -\; the \; limit \; of \; the \; top \; value \; base \; sequence ;]

The self similarity block of rank k of the euclidean fractal

For any four complex numbers u,v,w and z shaping a trapezoid let us consider the entity defined by the following elements:

the two base endpoints

[;\tilde{\alpha}_{k+1} \; and \; \tilde{\beta}_{k+2};]

the two top endpoints

[;\tilde{\beta}_{k+1} \; and \; 2\cdot \tilde{\beta}_{k+2} - \tilde{\alpha}_{k+2};]

the top line

[;\delta(\tilde{\beta}_{k+1}, 2 \cdot \tilde{\beta}_{k+2} - \tilde{\alpha}_{k+2});]

the parallelism master line

[;\delta(\tilde{\alpha}_{k+1}, \tilde{\beta}_{k+1});]

the top value

[;\beta^{(k)} = \overline{\sigma}(\tilde{\alpha}_0,\beta) \cap \sigma(\tilde{\beta}_{k+1}, 2 \cdot \tilde{\beta}_{k+2} - \tilde{\alpha}_{k+2});]

where:

[;\beta \; - \; defined \; as \; above;]

[;\overline{\sigma}(z_1,z_2) \; the \; closed \; complex \; line \; segment \; defined \; by \; z_1 \; and \; z_2;]

Moreover, the self similarity block of rank k is by itself an euclidean fractal main block.
Now for its link to the euclidean summation, consider the euclidean fractal main block defined by u=0,v=i,w=1+i and z=1. (suggestive figure pending)
Next: Fibonacci decomposition of n

Discrete connections (part V)

This part will deal mainly with the constructive elements of a fractal class derived from the conjectured asymptotic nature of the euclidean summation.
First some basic sequences and functions:

r-golden ratio builder

[;g_0^r=r, \; g_{n+1}^r = 1 + \frac{1}{g_n^r};]

upward shifted by r identity

[;u_n^r=n+r;]

upper ratio coefficient

[;\overline{\lambda}:[0,\infty) \rightarrow (0,1], \; \overline{\lambda}(x)=\frac{1}{1+x};]

where r>0 is a real number.

Let us consider some properties of the above sequences and functions:

[;\lim_{n\rightarrow \infty}\overline{\lambda}(g_n^r) = 1-\phi, \sum_n (-1)^n \cdot \prod_{i=0}^{n} \overline{\lambda}(g_i^r) \; convergent;]

[;\lim_{n \rightarrow \infty} \overline{\lambda}(u_n^r) = 0, \prod_n (1 - \overline{\lambda}(u_n^r)) \; convergent \; to \; 0;]

For the upward shifted by r identity, the conclusions are self evident due to:

[;\overline{\lambda}(u_n^r) = \frac{1}{1+n+r};]

and

[;\prod_{i=0}^{n} (1 - \overline{\lambda}(u_n^r)) = \frac{r}{1+n+r};]

For the r-golden ratio builder, the first conclusion's proof is based upon the relative positions of r and the golden ratio.

Indeed, if r is equal to the golden ratio then the r-golden ratio builder is stationary (and equal to the golden ratio).

From the two left cases let's consider the case r is smaller than the golden ratio. With this assumption we get:

[;r^2 -r -1 < 0 \Rightarrow g_1^r - g_0^r = -\frac{r^2-r-1}{r} > 0;] 

By means of mathematical induction one can prove that the subsequences of even index and odd index terms of the r-golden ratio are respectively increasing and decreasing. Since both sequences fall between the two first terms of the sequence results that they are both convergent to respectively g and h. 

We get successively:

[;\left\{ \begin{array}{rcl} g & = &1+\frac{1}{h}\\ h & = &1+\frac{1}{g} \end{array} \right. \Leftrightarrow \left\{ \begin{array}{rcl} g & = &1+\frac{1}{1+\frac{1}{g}} \\ h & = & 1+\frac{1}{g} \end{array} \right. \Leftrightarrow;]
[;\left\{ \begin{array}{rcl}g & = & \frac{2\cdot g +1}{g+1} \\ h & = & 1 + \frac{1}{g}\end{array}\right. \Leftrightarrow \left\{ \begin{array}{rcl} g^2 -g -1 & = & 0\\ h & = & 1 + \frac{1}{g} \end{array} \right. \Leftrightarrow;]
[;\left\{ \begin{array}{rcl}g & = & \varphi \\ h & = & 1 + \frac{1}{g}\end{array}\right. \Leftrightarrow \left\{ \begin{array}{rcl} g & = & \varphi \\ h & = & \varphi \end{array} \right.;]

Therefore the entire sequence is convergent to the golden ratio. Since the golden ratio is not equal to 1 results that:

[;\sum_n (-1)^n \cdot \prod_{i=0}^{n} \overline{\lambda}(g_i^r);]

is convergent.

Having these sequences and functions completely described let us consider the two mechanisms we will use in order to define the previously mentioned class of fractals:

The top value base sequence

For any four complex numbers u,v,w,z shaping a trapezoid and the sequences:

[;(\alpha_n)_{n\ge 0}, \; (\beta_n)_{n\ge 0};]

defined by:

[;\alpha_0=u, \; \beta_0=v, \beta_1=w,\; \alpha_1=z;]

and

[;\left\{ \begin{array}{rcl} \alpha_{n+2} & = & (1 - \overline{\lambda}(g_n^r))\cdot \alpha_{n+1}+ \overline{\lambda}(g_n^r) \cdot \alpha_{n} \\ \beta_{n+2} & = & (1 - \overline{\lambda}(g_n^r))\cdot \alpha_{n+1}+ \overline{\lambda}(g_n^r) \cdot \beta_{n} \end{array} \right. ;]

we have that:

[;(\alpha_n)_{n\ge 0} \rightarrow \alpha;]

The self-similarity base sequence

For any four complex numbers u,v,w,z shaping a trapezoid and the sequences:

[;(\tilde{\alpha}_n)_{n\ge 0}, \; (\tilde{\beta}_n)_{n\ge 0};]

defined by:

[;\tilde{\alpha}_0=u, \; \tilde{\beta}_0=v, \tilde{\beta}_1=w,\; \tilde{\alpha}_1=z;]

and

[;\left\{ \begin{array}{rcl} \tilde{\alpha}_{n+2} & = & (1 - \overline{\lambda}(u_n^r))\cdot \tilde{\alpha}_{n+1}+ \overline{\lambda}(u_n^r) \cdot \tilde{\alpha}_{0} \\ \tilde{\beta}_{n+2} & = & (1 - \overline{\lambda}(u_n^r))\cdot \tilde{\alpha}_{n+1}+ \overline{\lambda}(u_n^r) \cdot \tilde{\beta}_{0} \end{array} \right. ;]

we have that:

[;(\tilde{\alpha}_n)_{n\ge 0} \rightarrow \tilde{\alpha}_0;]

For both sequences r is the scaling ratio of the two parallel edges of the trapezoid i.e.:

[;(u-v)=r\cdot (z-w);]

The construction of the above two sets of sequences is better depicted by the following figures:

and

Next: The euclidean fractal class

Discrete connections (part IV)

Before dealing with the major results, let us consider the following:

 Intermediate recurrence

[;\frac{n}{2}<k<\frac{2\cdot n}{3} \Rightarrow;]

[;\tau_1(n,k)=k+\tau_1(n-k,2\cdot k - n);]

Its proof consists in applying the outer row recurrence first for n and k and then for k and n-k.

The first major result consists, as the above one, from two formula iterations:

Asymptotic expansion

a)

[;\frac{F_{2 \cdot m}}{F_{2 \cdot m + 1}} \cdot n <k< \frac{F_{2 \cdot m - 1}}{F_{2 \cdot m}} \cdot n \Rightarrow;]

[;\tau_1(n,k) = (\sum_{i=1}^{2 \cdot m - 1}(-1)^{i+1} \cdot F_{i}) \cdot n + (\sum_{j=2}^{2\cdot m} (-1)^{j+1} \cdot F_{j}) \cdot k +;]

[;\tau_1(F_{2 \cdot m-1} \cdot k - F_{2\cdot m - 2} \cdot n, F_{2 \cdot m - 1} \cdot n - F_{2 \cdot m} \cdot k);]

b)

[;\frac{F_{2 \cdot m}}{F_{2 \cdot m + 1}} \cdot n <k< \frac{F_{2 \cdot m + 1}}{F_{2 \cdot m + 2}} \cdot n \Rightarrow;]

[;\tau_1(n,k) = (\sum_{i=1}^{2 \cdot m }(-1)^{i+1} \cdot F_{i}) \cdot n + (\sum_{j=2}^{2\cdot m + 1} (-1)^{j+1} \cdot F_{j}) \cdot k +;]

[;\tau_1(F_{2 \cdot m - 1} \cdot n - F_{2 \cdot m} \cdot k, F_{2 \cdot m+1} \cdot k - F_{2\cdot m } \cdot n);]

where 

[;F_{1} = F_{2}=1;]

[;F_{m+2}=F_{m+1} + F_{m};] 

stand for the terms of the Fibonacci sequence, and by natural convention:

[;F_{0} = 0;]

The proof follows by mathematical induction, the base case being ensured by the outer row recurrence  (for a)) and the intermediate recurrence (for b)). For the inductive step we will suppose that a) and b) hold for n arbitrarily fixed m. Through the outer row recurrence results that a) holds for m+1 as well and in a similar fashion b) holds for m+1 as well, thus concluding the inductive reasoning.
Since from the previous part we have that:

[;\frac{\tau_2(n)}{n} < 1;]

and for a conveniently chosen m, via the asymptotic expansion we have that:

[;\frac{\tau_2(n)}{n} > \frac{F_{2\cdot m + 1} - 1}{ F_{2 \cdot m + 1}};]

we can now state that:

[;(\frac{\tau_2(n)}{n})_{n \ge 1} \rightarrow 1;]

There is also another gain (from the asymptotic expansion), from the perspective of the positional peak: if we squeeze k such that the fraction n/k becomes closer and closer to the golden ratio we get values of the euclidean summation pretty close to n. Alas we can only conjecture for now that:

[;(\frac{\tau_3(n)}{n})_{n \ge 1} \rightarrow \phi;]

where:

[;\phi = \frac{1}{\varphi} \approx 0.618;]

is called the golden ratio conjugate.

Next: Fractal candidate building blocks

Discrete connections (part III)

For the positional peak, its boundaries are straightforward (definition, inner row  recurrence and lower boundary):

[; \frac{n}{2}<\tau_3(n)<n \; \forall \; n \ge n_{\tau_3};]

For the peak, it's a two step argument. For the lower bound we consider two cases: n odd and respectively n even. For every such case we take a conveniently chosen pair, compute the euclidean summation and truncate it up to a suitable value:

 [; n = 2 \cdot k + 1 \Rightarrow ;]

[; \tau_1(n,k+2) = n-(k+2) + \tau_1(k+2, k-1) \Rightarrow ;]

[; \tau_1(n,k+2) \ge k-1 + 3= k+2 > k + \frac{1}{2} = \frac{n}{2} ;]

[; n=2\cdot k \Rightarrow ;]

[;\tau_1(n,k+1) = n-(k+1) + \tau_1(k+1, k-1) \Rightarrow ;]

[; \tau_1(n,k+1) \ge k-1 + 2= k+1 > k = \frac{n}{2};]

Here also the inequality holds from a rank on, due to the approximations used.

For the upper bound, our reasoning will follow the rules of the mathematical induction:

 base case

[;\tau_1(1,0)=0<1;]

inductive step (n arbitrarily fixed)

[;\tau_1(k,r)<r \; \forall \; k,r \; such \; that \; n>k>r \Rightarrow ;]

[;\forall \; k<n \Rightarrow \exists \; q,r \; such \; that \;q \ge 1, k>r, n=q\cdot k + r  \Rightarrow ;]

[;\tau_1(n,k) = r + \tau_1(k,r) < r + k \le r + q \cdot k = n;]

thus concluding our reasoning.

We get in conclusion:

[; \frac{n}{2}<\tau_2(n)<n \; \forall \; n \ge n_{\tau_2};]

Next: Asymptotic behaviors of peak and positional peak.

Discrete connections (part II)

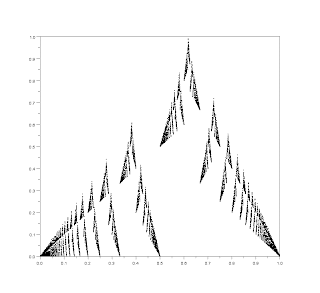
First, some Scilab-powered graphic suggesting the conjectured fractal nature of the euclidean summation:

The normalized euclidean summation (m=10000 and 0<n<10000)

But science relies upon facts, so let's begin by listing some of the basic properties of the euclidean summation:

Lower boundary

[;\tau_1(n,k) = 0 \Leftrightarrow (k=0)$ or $((k\neq 0)$ and $(k|n));]

Homogeneity

[;\tau_1(p\cdot n, p\cdot k) = p \cdot \tau_1(n,k);] 

Column periodicity

[;m_1\equiv m_2\pmod{n}$ $\Rightarrow$ $\tau_1(m_1, n) = \tau_1(m_2,n);]

Outer row recurrence

[;\frac{n}{2}<k<n \Rightarrow \tau_1(n,k) = n-k + \tau_1(k,n-k);]

Inner row recurrence

[;\frac{n}{2}<k<n \Rightarrow \tau_1(n,k) = n-k + \tau_1(n,n-k);]

Diagonal periodicity

[;\frac{n}{2}<k<n \; and \; 0 \le r < (n-k) \Rightarrow ;]

[;\tau_1(n + p \cdot (n-k) + r, k + p \cdot (n-k) + r) = \tau_1(n+r, k+r) ;]

Next: Boundaries for peak and positional peak

Discrete connections (part I)

As you probably expected, all the previous subjects (Fibonacci sequence, golden ratio and fractals) are the pieces of a larger puzzle: a set of mathematical tools describing the nature of numbers. Their connection comes from a rather unexpected place: the greatest common divisor (the largest number dividing both numbers) algorithm as described by Euclid.
The algorithm states that in order to compute the gcd of two natural numbers m and n it suffices to compute the quotient q and remainder r from their integer division, and if r is non-zero repeat the procedure for n and r. The last non-zero remainder obtained in this manner, or n if no such remainder existed, is the gcd.
The subject of the Euclid's algorithm was intensively studied throughout the history of mathematics, one of the most interesting results (involving also Fibonacci numbers) being Lamé's theorem describing the number of steps it takes to compute the gcd for a given pair or numbers a and b.
The novel (to be read independent, since I consider that most of the time we reinvent the math) approach considers a rather unexplored characteristic of the algorithm, that of the summation of the remainders.
Thus let us define the euclidean summation, euclidean summation peak and euclidean summation positional peak by the following:

[; \tau_{1}(m,n) = m\mod n + \tau_{1}(n, m\mod n) ;]
[; \tau_{2}(n)=\max\{\tau_{1}(n,k)| 0\le k \le n\};]
[; \tau_{3}(n) = \max \{k|0 \le k \le n \; and \; \tau_{1}(n,k)=\tau_2(n) \} ;]

where mod is the extended modulus operator of two natural numbers, i.e. the remainder of their integer division, if the divisor is non-zero and zero otherwise.
The purpose of this blog-based article is to conjecture (and maybe someday prove) the fractal nature of the sum of remainders, fully describe a strong candidate for it and some tools to describe the common properties of the two.
Hope you'll find it interesting enough to stop by every now and then for updates.

Fractals and life (part I)

Well, these are a special breed of mathematical beasts, they are ever growing collections of dots and no matter how deep you zoom them in you'll get about the same picture as you got when looking at the original.
As an example, one of the most intuitive ones, we will consider Sierpinski's triangle: let us take a triangle with all sides equal and join the middles of its sides. We thus get four smaller triangles. Lets cut off the one in the center. We now have only three triangles in the corners, and repeat for each one of them the same procedure: join middles and cut the center triangle. If we infinitely repeat the procedure we would obtain something that looks like this:

Where does life use these kind of tools? Frosted window patterns, broccoli, shattered compact discs, Scandinavian fjords and the list goes on. 

References:

Artwork: http://www.zeuscat.com/andrew/chaos/sierpinski.html

Examples: http://en.wikipedia.org/wiki/Main_Page

Golden ratio and life (part I)

Warning: Starting with this blog you may need some additional magic: in order to typeset mathematical formulas I used a script file named TeX THE WORLD. Consequently you may have to enable javascript in your browser (Greasemonkey and the same user script). Sorry about the inconvenience, but this way maths look better.

As it's name states, the golden ratio has everything to do with geometry and aesthetics. It was defined by the following property: "Given a line segment of length c, how can we divide it in two sub-segments of lengths a and b (c=a+b, a > b) such that the ratio of the large over the small equals the ratio of the segment over the large?" Otherwise said:

[; \varphi = \frac{a}{b} = \frac{c}{a} ;]

Now, replacing c by the sum of a and b, we get:

[; \varphi = \frac{1 + \varphi}{\varphi} ;]

hence:

 [; \varphi = \frac{1+\sqrt{5}}{2} \approx 1.618 ;]

This proportion was deeply engraved in ancient (the Parthenon), Renaissance (Mona Lisa) and modern (The Sacrament of the Last Supper) masterpieces of painters and architects, and all for a reason: mathematics ARE aesthetically pleasing.
And coincidences don't stop here: remember the Fibonacci sequence? Let's consider consecutive terms ratios and place them like this:

[;\frac{1}{1}, \frac{3}{2}, \frac{5}{8}, ... ? ... , \frac{13}{8},\frac{5}{3},\frac{2}{1};]

We get two sequences, an increasing one and a decreasing one, both leading to ... the golden ratio. So, if you want to use golden ratio-like proportions, the Fibonacci numbers are your best choice, no need for tedious square roots.

Fibonacci and life (part I)

I chose Fibonacci's sequence as a starting point of my blog for several reasons:

1. It's plain (no tricks);
2. It branches into our day-to-day living in surprising ways.

So let's give it a go: 1, 1, 2, 3, 5, 8, ... can you see the pattern? Yup! You got it, starting from 2 all the terms of the sequence are the sum of the previous two (1+1=2, 1+2=3, ...). Now where does real life kick in? You've all heard about the saying "breeding like rabbits", but never imagined the mathematical extents of it:

• first we buy a male rabbit and a female rabbit (no gender discrimination intended) (1 pair);
• the first month they have no baby rabbits (not mature enough) (1 pair);
• the second month they have two baby rabbits, a male and female (2 pairs);
• the third month the original pair has two more baby rabbits (male and female), their first babies are not mature yet so they have none (3 pairs); 
• the fourth month both the original pair and their first pair of babies (yeah, I know, they mate family, the animals!) have each one pair of babies (5 pairs);
• a.s.o. many, many rabbits.

Luckily for us there is such thing as natural selection through predators, disease or genetics and the math does not ensure rabbits' world domination.

Let there be science

Knowledge is power, so I decided to let it flow. Bare with me since this is the first of many. I will try to make it as scientific as it gets and be receptive to constructive criticism.